Imagine earning $1 million, just for solving math problems. However, these aren’t your regular problems, these are proving mathematical problems, which means being on the front line of math, allowing mathematicians to go even further into the world of numbers, shapes, graphs, equations, and the other things you learned some in class. This article can not possibly help to fully explain the problems, let alone the math setting each of them up. However, this article will give some info, especially what it affects / why it is important. Each section below is one of the seven Millenium Prize Problems, and each heading is a link to a more in-depth explanation of the problem.
Yang-Mills and Mass Gap
This problem is of how math relates to physics, specifically, quantum physics. An old theory describes particles (the things that make up everything, including electrons, photons, light, and quarks – the bits that make up protons and neutrons which in turn make atoms) in such a way that it presents a huge problem. There is some number – the mass gap – that is critical to completing this understanding of particle physics. Whoever can find this mass gap will be a winner.
Riemann Hypothesis
This theorem is based on the interesting zeta function,
ζ(s) = 1 + 1/2s + 1/3s + 1/4s + …
This equation graphs to 3D space, but every solution to ζ(s) = 0 lies on a straight verticle line. The behavior of this line is very closely related to the distribution of primes (numbers that are only divisible by themselves and 1). Keep in mind, our current understanding of primes is that they have no pattern. This is critical to cybersecurity, as the field uses prime numbers’ randomness. The hypothesis is based on these solutions. If it is proven or unproven, it will have radical effects on cybersecurity, aka, all of the internet
P vs NP Problem
This is a brain-twister. It is easy to have a problem and check if an answer is an actual solution, but it can be much harder to find a solution. Figuring out how much harder it is is the solution to this problem
Navier–Stokes Equation
The Euler and Navier-Stokes equations can describe how fluids and air move. However, we have little understanding of what they mean. Give a better meaning to these complex equations and you’ll be a winner. The first equation is the same as F=ma, just applied to liquids and gasses with additional forces on it. The second equation says that liquids can’t be compressed.
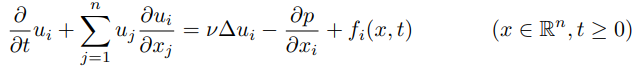
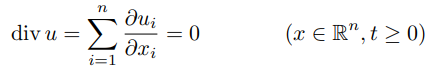
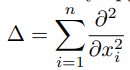
Hodge Conjecture
A while ago, mathematicians (including Hodge) came up with a very powerful idea involving the math of shapes, and topology. While this idea is very complex, it can be used in a great many ways, and a multitude of uses and generalizations have come from it. However, along the way, we lost sight of one of the central ideas of the idea. This conjecture is set to try and find this central proof.
Poincaré Conjecture
In 1904 the French mathematician Henri Poincaré asked a question that seriously rocked the boat. Mathematicians were trying to generalize spheres in multiple dimensions. They saw that a 2D sphere (a circle) was similar to a 4D sphere. However, they couldn’t prove the same property for 3D spheres.
Birch and Swinnerton-Dyer Conjecture
Supported by much experimental evidence, this conjecture relates the number of points on an elliptic curve mod p to the rank of the group of rational points. Elliptic curves, defined by cubic equations in two variables, are fundamental mathematical objects that arise in many areas: Wiles’ proof of the Fermat Conjecture, factorization of numbers into primes, and cryptography, to name three.